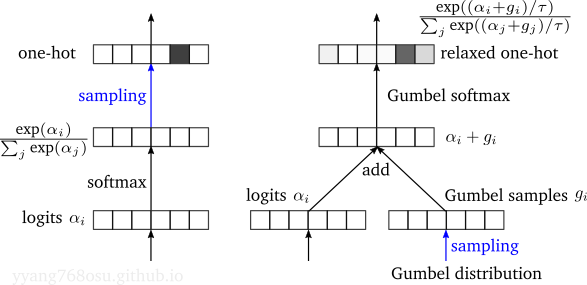
Gumbel max and Gumbel softmax
Before we talk about Gumbel distribution, let’s refresh our knowledge on exponential distribution. It is well-known that the exponential distribution is min-stable: the min of \(n\) I.I.D. exponential random variables \(X_i\sim \text{Exp}(\lambda_i), i=1,2,\ldots, n\) is also exponentially distributed with decay rate \(\sum_{1\leq i\leq n} \lambda_i\), as can be seen from the equation below.
\[\begin{align*} P(\min_{1\leq i \leq n} X_i > x) &= \prod_{1\leq i\leq n} P(X_i>x) = e^{-\sum_{1\leq i\leq n}\lambda_i x} \end{align*}\]A lesser known property is that the arg-min of exponential variables is a multinomial distribution with event probabilities \(\left(\frac{\lambda_1}{\sum_{i}\lambda_i}, \ldots, \frac{\lambda_n}{\sum_{i}\lambda_i}\right)\):
\[\begin{align*} &P(\arg\min_{1\leq i\leq n}X_i =k)\\ =&\int_0^\infty P(\arg\min_{1\leq i\leq n} X_i = x | X_k=x)f(X_k = x)dx\\ =&\int_0^\infty \prod_{i=1\to n, i\not=k} e^{-\lambda_i x} \lambda_k e^{-\lambda_k x} dx\\ =&\frac{\lambda_k}{\sum_{i=1\to n} \lambda_i}. \end{align*}\]As we will see shortly, this property directly leads to the Gumbel max trick.
Gumbel max trick
Assume that we are given a multinomial (a.k.a. categorical) distribution with unnormalized event probabilities \(\lambda_i, i=1\to n\) (i.e., \(\sum_{i=1}^n\lambda_i\not=1\)), the above property provides us a way to sample from the distribution without the need for normalization:
- draw \(n\) samples from an exponential distributions with decay rate of \(1\)
- scale the value of these \(n\) samples with \(1/\lambda_i\) for \(i=1\to n\).
- take the index of the minimum of the scaled samples
To be more precise, we are utilizing the fact that
\[\begin{align*} &\arg\min_{1\leq i\leq n} \left(\frac{1}{\lambda_i}s_i\right) \sim \text{Multinomial}\left(\frac{\lambda_1}{\sum_{i}\lambda_i}, \ldots, \frac{\lambda_n}{\sum_{i}\lambda_i}\right)\\ &\text{where } s_i\sim \text{Exp}(1), \forall i. \end{align*}\]For the case of soft-max operation, we have direct access to the log of the unnormalized probabilities \(\alpha_i=\log \lambda_i\) (multinomial logit), instead of the unnormalized probabilities itself. In this case, we can modify the above equation as below
\[\begin{align*} &\arg\min_{1\leq i\leq n} \left(\frac{1}{e^{\alpha_i}}s_i\right) \sim \text{Multinomial}\left(\frac{e^{\alpha_1}}{\sum_{i}e^{\alpha_i}}, \ldots, \frac{e^{\alpha_n}}{\sum_{i}e^{\alpha_i}}\right)\\ &\text{where } s_i\sim \text{Exp}(1), \forall i. \end{align*}\]One observation is that the left hand side of the above equation is invariant to any linear transform. The Gumbel-max trick is obtained by taking \(-\log(\cdot)\) operation to the right-hand-side, in which case \(-\log(\text{Exp}(1))\) is a standard Gumbel distribution, leading to the equation below
\[\begin{align*} &\arg\max_{1\leq i\leq n} \left(\alpha_i+g_i\right) \sim \text{Multinomial}\left(\frac{e^{\alpha_1}}{\sum_{i}e^{\alpha_i}}, \ldots, \frac{e^{\alpha_n}}{\sum_{i}e^{\alpha_i}}\right)\\ &\text{where } g_i\sim \text{Gumbel}(\text{location}=0, \text{scale}=1), \forall i. \end{align*}\]This provides us a way to obtain samples directly from the logits without going through the exponentiate-and-normalization step
- draw \(n\) samples from a standard Gumbel distributions with location of \(0\) and scale of \(1\).
- add the values of the \(n\) samples to the logits.
- take the index of the minimum of the \(n\) summations.
Essentially, the Gumbel max trick converts the sampling operation from a categorical/multinomial distribution into an argmax operation. The sampling process can be expedited if we pre-calculate and store a stream of Gumbel samples.
Gumbel softmax